The hysteresis of vibe coding

Hysteresis is a weird and kind of ill-defined term from nonlinear dynamics (which is the study of systems whose outputs(s) are nonlinear functions of their input(s).) The gist is that a hysteretic system depends on past values of its input as well the present value. You can't simply calculate the output of the system given the input; you need to know the history of that input as well.

As a simple example, consider this system that consists of a curve with two wells, a marble that sits in one of the wells, and a control parameter \(c\) that determines the shape of the curve:

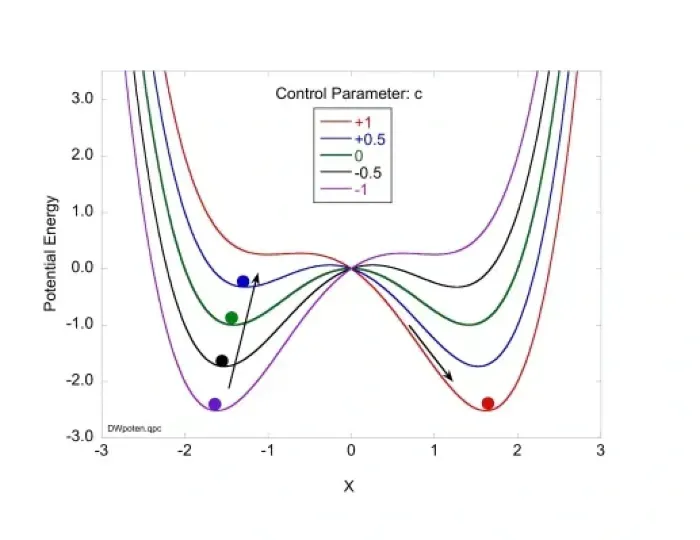
As you can see, \(c\) determines how deep the wells are relative to each other. When \(c\) is at 0, the wells are equally deep and the curve is symmetric. Increasing \(c\) moves the left well up and to the right and the right well down and to the right; decreasing \(c\) does the opposite.

There's a single marble that starts in the left well. When \(c\) gets high enough the marble will roll out of the left well and into the right one. Pushing \(c\) low enough will roll the marble back into the left well. The marble is a little heavy, so if we leave the system alone it will slowly deepen the well it's in (i.e. it will raise or lower \(c\).)

Here's a graph showing how the \(X\) coordinate of the marble varies as we vary \(c\):

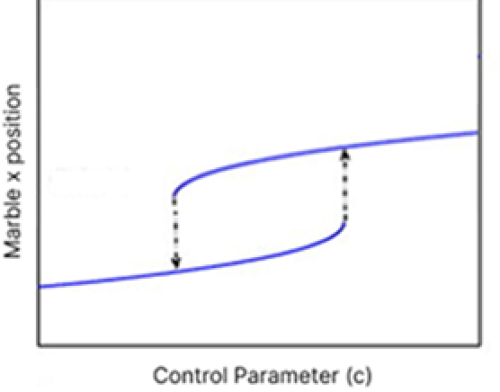
Take a second to make sure you understand how this graph results from the dual-well system described above. When the marble is in the left well, changing \(c\) moves us along the bottom curve. When the marble is in the right well, changing \(c\) moves us along the top curve. The dotted arrows represent the points where the marble moves from one well to another.

Notice that, in general, knowing the current value of \(c\) won't tell us where the marble is! This is how we know the system has hysteresis. If \(c\) is 0, the position of the marble depends on which well it's in, and to know that, we need to know what the past values of \(c\) were, since we need to know if it went high or low enough to move the marble between wells.

The loop structure of this graph is a telltale sign of hysteresis.

Our system doesn't stay still at rest; the weight of the ball pulls down its well. This means that there are forces pushing the system along one of the two curves in the loop, away from the transition points. Here's the same graph with some arrows showing those forces:

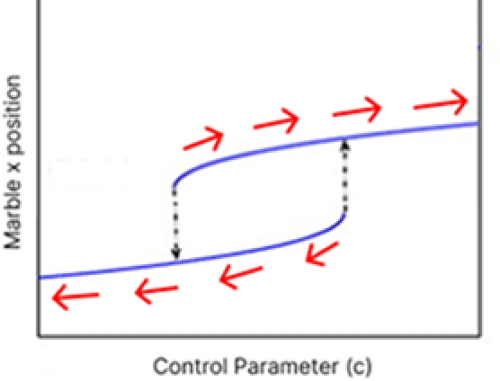
This creates a phenomenon known as bistability (a common companion to hysteresis). The system has two stable modes, and the transitions between the modes are hard to reverse - for example, once you've moved the ball from one well to another, moving it back takes a lot of effort. It's not enough to move \(c\) back across the threshold that triggered the transition; you have to go much further (there are some scary but illustrative examples of this in climate modeling.)

Vibe coding has its own kind of hysteresis:

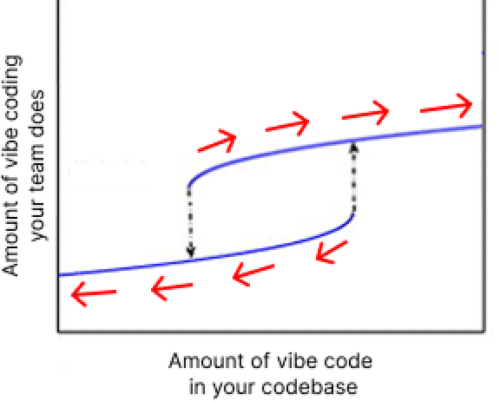
Introducing vibe-coding to a hand-crafted codebase means moving forward along the bottom line, left to right. Moving away from vibe-coding and going back to doing things by hand means moving backward across the top line, right to left. In both cases you're pushing against forces that want to keep you where you are.

Let's take a closer look at each curve, starting with the bottom one. Say you have a codebase that is mostly or completely hand-crafted.

I'm using hand-crafted here to mean code that is hand-written and reasonably well-structured - doesn't have to be perfect. As we'll see in a second, a hand-written rat's nest may as well be vibe code.

Clean code is explicitly meant to be easy for other developers to understand and change. This is achieved through many patterns that are helpful to us humans and somewhat vestigial to machines - design systems, modularity and encapsulation, separation of concerns, clear and simple data flow, separation of stateful and stateless code, sensible and consistent naming, and so on. If you're an experienced developer working on a relatively clean codebase, you can probably make changes faster and more precisely than an AI could while at the same time maintaining or improving architectural quality. Trying to coax an LLM into doing exactly what you would do is a net time sink. Attempts to vibe code anything but the smallest fixes will likely end in exasperation as you realize it's more effective to write everything yourself. This force pushes you backwards (left and down.)

In addition, hand-crafting a codebase usually results in a high degree of understanding and familiarity across the team. Since vibe coding pays off the most when you need to quickly make changes to code you don't know well, broad adoption only makes sense when there's enough vibe code to erode the collective knowledge base past a critical point. This is why the mode transition from the bottom line to the top happens so far to the right.

Now, the top curve: let's assume the team has been vibe coding for a while and the code base is mostly AI-generated. Vibe coding tools are fast and convenient, but imprecise on a macro level. You could, in theory, keep hounding your agents until they get the architecture right, but this can take a lot of time, and if you've committed to vibe coding you're probably expected to keep velocity high. The incentive is to accept any code that works, even if it's not pristine. You could fix things after the fact, but you won't: it takes a lot of time and effort (more than you can spare) to tidy up a mature codebase, and trying to write clean code on top of janky code almost never works (it's like trying to build a house on a busted foundation.) In this case letting the AI drive is clearly the right policy; an LLM will always be able to parse and manipulate a plate of spaghetti better than you can, and it doesn't really matter if it's adding to the mess when doing things yourself would be untenably slow. These dynamics all push you forwards (right and up).

Meanwhile, you and your team have a relatively shallow understanding of the code you're producing, both because it's not particularly organized and because you didn't write it yourself. Speed pressure means you're probably spending more time studying the system's outputs (i.e. verifying that it works) than its internals. This means if you want to start making changes by hand, you'll have to invest in cleaning up your code and building team-wide familiarity with the codebase before you can even get close to parity with AI. This requires a lot of hands-on time in the guts of the system, so the transition from top to bottom is way off to the left.

Beware the vibe coding hysteresis loop. If you want to vibe code, vibe code, and if you don't, don't, but you shouldn't try to split the difference. And you should recognize that your choice probably won't be as reversible as you think!